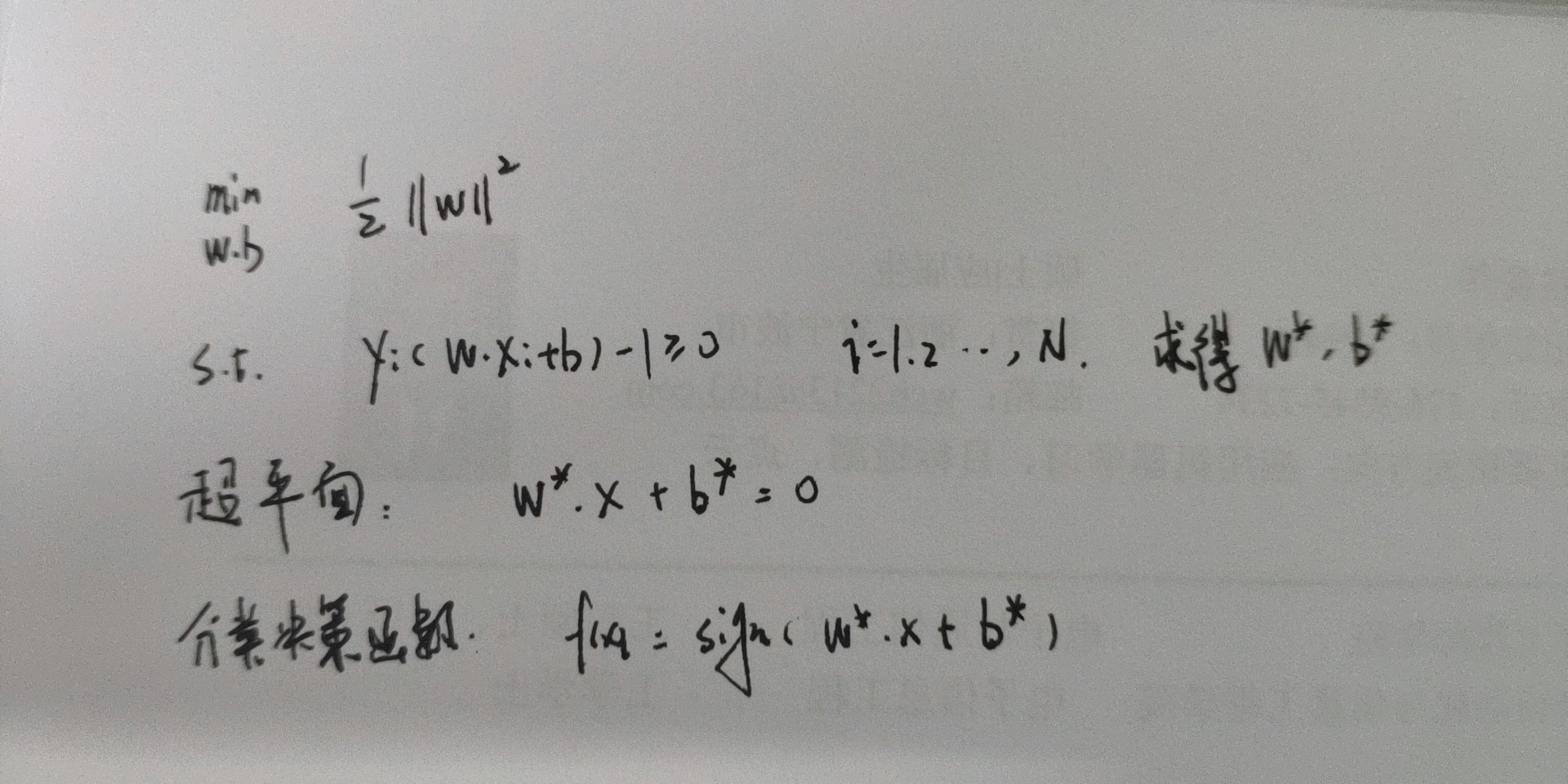线性可分支持向量机和非线性支持向量机
线性可分又分为硬间隔最大化和软间隔最大化(正则化)


- 硬间隔最大化
- 软间隔最大化
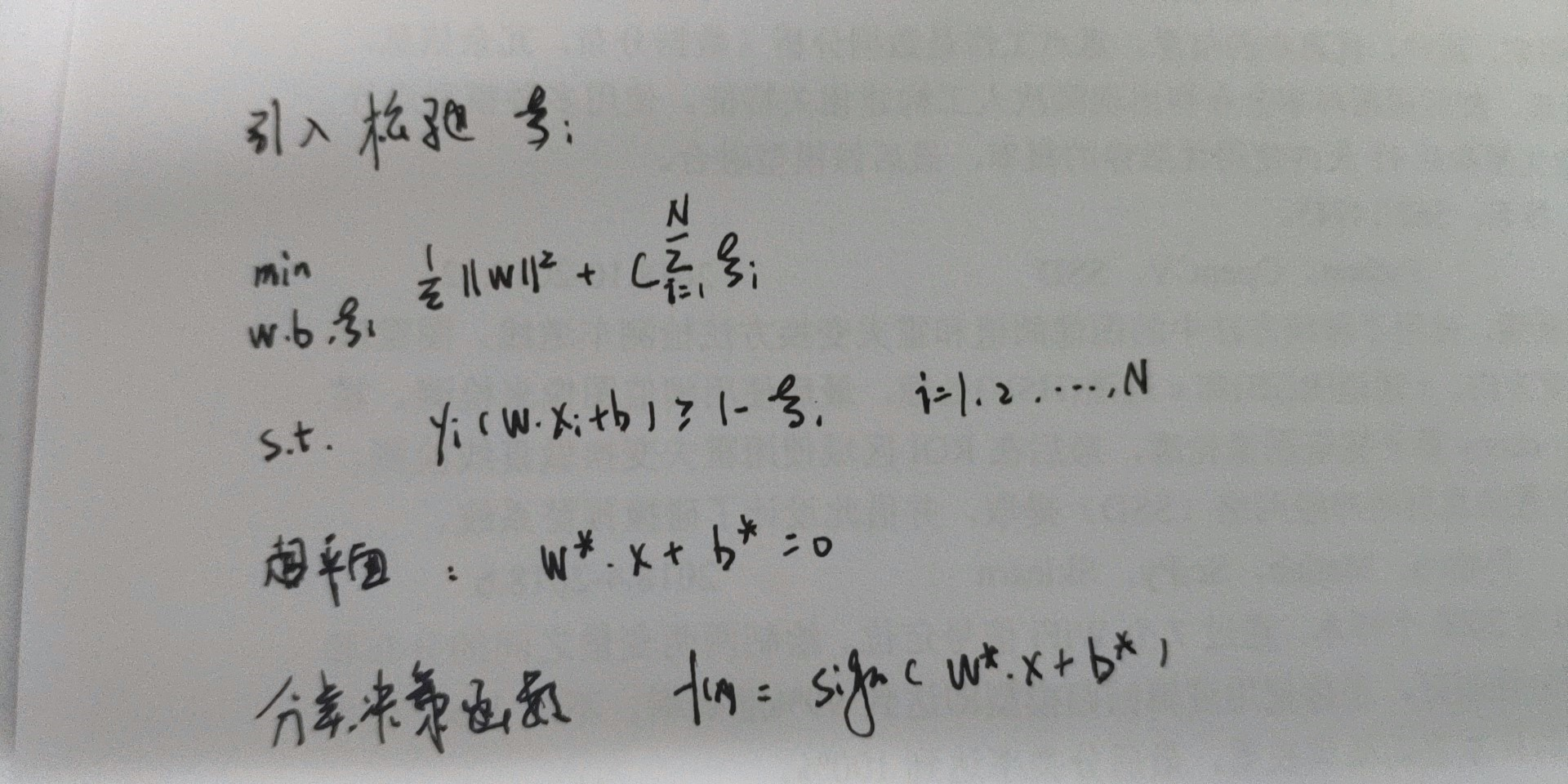
- 合页函数

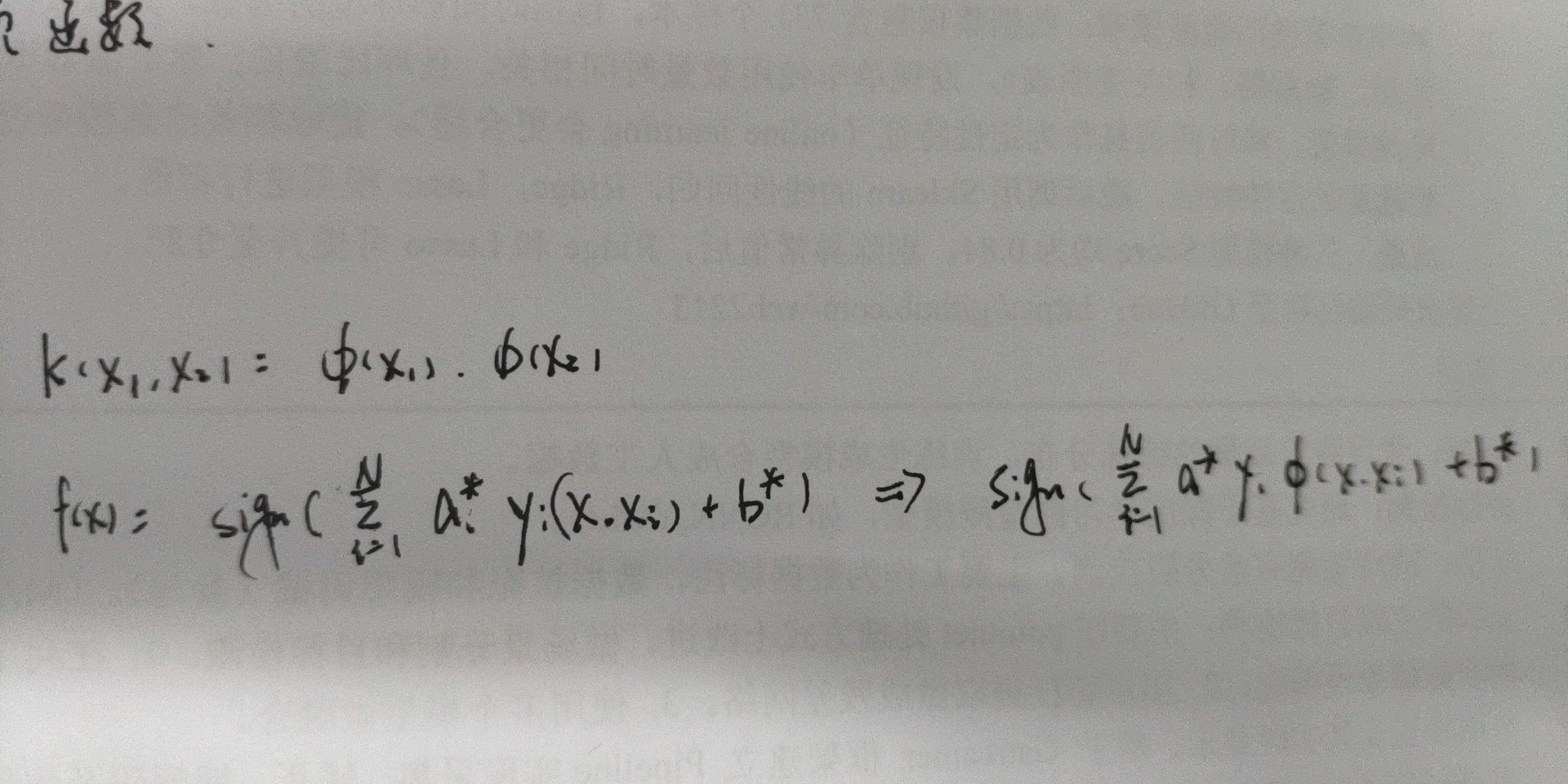
- 通过将输入空间内线性不可分的数据映射到一个高纬的特征空间内使得数据在特征空间内是可分的
- 核函数K为正定核的充要条件
- 如果满足上述条件,可以构成一个内积封闭的希尔伯特空间,必能找到合适的映射Φ(x)。
- 种类
- 线性核函数 κ(x,xi)=x⋅xi
- 即无核,线性可分场景。可以先用这种试试
- 多项式核函数
- 多项式核函数可以实现将低维的输入空间映射到高纬的特征空间,但是多项式核函数的参数多,当多项式的阶数比较高的时候,核矩阵的元素值将趋于无穷大或者无穷小,计算复杂度会大到无法计算。
- 高斯(RBF)核函数
- 高斯径向基函数是一种局部性强的核函数,其可以将一个样本映射到一个更高维的空间内。一般都用这用
- κ(x,xi)=exp(−||x−xi||2δ2)
- sigmoid核函数
- κ(x,xi)=tanh(η<x,xi>+θ)
- 采用sigmoid核函数,支持向量机实现的就是一种多层神经网络。
- 使用场景
- 在样本数量不变,差不多的前提下
- 特征数量比较多(和样本数量差不多),则选用LR或者线性核的SVM;
- 特征的数量小(样本的数量正常),则选用SVM+高斯核函数;
- 特征的数量小,且样本数量足够,则需要手工添加一些特征从而变成第一种情况